| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 5 (Before Exercise 12.1) | Exercise 12.1 | |
Chapter 12 Statistics
Welcome to the solutions guide for Chapter 12, "Statistics," from the latest Class 9 NCERT mathematics textbook for the academic session 2024-25. In an increasingly data-driven world, the ability to effectively organize, represent, and interpret data is a crucial skill. This chapter focuses on the fundamental methods used in statistics to handle raw information and present it in meaningful ways, primarily through tables and graphical representations. These solutions provide comprehensive, step-by-step assistance for mastering these essential data presentation techniques.
The initial challenge in statistics often lies in managing raw, collected data. The solutions begin by demonstrating systematic methods for presentation of data. This includes organizing raw data into structured formats, particularly frequency distribution tables. Clear explanations are provided for constructing both ungrouped frequency tables (listing individual values and their frequencies) and, more importantly for larger datasets, grouped frequency distribution tables. Key concepts associated with grouped data are clarified:
- Classes or Class Intervals: The ranges into which data is grouped (e.g., 0-10, 10-20).
- Class Size or Class Width: The difference between the upper and lower class limits.
- Class Marks (Midpoints): The midpoint of a class interval, calculated as $\frac{\text{Upper limit} + \text{Lower limit}}{2}$.
- Distinction between inclusive and exclusive class interval formats.
A major focus of this chapter is on the graphical representation of data, which allows for visual interpretation and comparison. The solutions provide detailed guidance on constructing key statistical graphs:
- Bar Graphs: Suitable for representing discrete data or comparing frequencies across distinct categories. Construction involves drawing bars of uniform width with heights proportional to the frequency.
- Histograms: Used specifically for representing continuous grouped data. Unlike bar graphs, there are no gaps between the bars in a histogram (representing the continuous nature of the data). The solutions provide step-by-step instructions for drawing histograms with uniform class widths, ensuring the area of each rectangle is proportional to the frequency of its class interval.
- Frequency Polygons: Another way to represent grouped frequency distributions, either by joining the midpoints of the tops of the bars in a histogram or by plotting points using the class marks and frequencies and connecting them with line segments. Solutions illustrate how to construct these polygons accurately.
Regarding the rationalized syllabus for 2024-25, Chapter 12, "Statistics" (formerly Chapter 14), in the Class 9 NCERT textbook has undergone significant changes. The focus is now primarily on the presentation of data in tabular form (frequency distributions) and graphical representation using Bar Graphs, Histograms (with uniform width), and Frequency Polygons. Notably, the section on calculating measures of central tendency (Mean, Median, and Mode) for ungrouped data has been removed from the Class 9 curriculum, deferred to Class 10. By engaging with these focused solutions, students can master the essential techniques for organizing data and constructing/interpreting key statistical graphs, building a strong foundation for future data analysis.
Example 1 to 5 (Before Exercise 12.1)
Example 1. In a particular section of Class IX, 40 students were asked about the months of their birth and the following graph was prepared for the data so obtained:
Observe the bar graph given above and answer the following questions:
(i) How many students were born in the month of November?
(ii) In which month were the maximum number of students born?
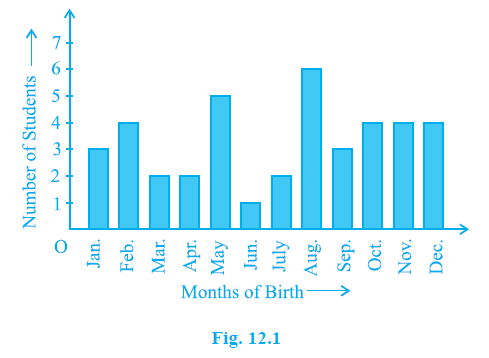
Answer:
Given:
A bar graph representing the birth months of 40 students in a section of Class IX.
To Find:
(i) Number of students born in November.
(ii) The month with the maximum number of students born.
Solution:
We need to observe the given bar graph to answer the questions.
The horizontal axis shows the months, and the vertical axis shows the number of students.
Part (i): How many students were born in the month of November?
Locate the bar corresponding to the month of November on the horizontal axis.
Read the height of the bar for November from the vertical axis (number of students).
The bar for November extends up to the mark indicating 4 students.
Therefore, the number of students born in November is 4.
The number of students born in the month of November is 4.
Part (ii): In which month were the maximum number of students born?
To find the month with the maximum number of students born, we need to identify the tallest bar in the graph.
By observing the heights of all the bars:
- January: 3
- February: 4
- March: 2
- April: 2
- May: 5
- June: 1
- July: 2
- August: 6
- September: 3
- October: 4
- November: 4
- December: 4
The maximum height is 6, which corresponds to the month of August.
Therefore, the maximum number of students were born in the month of August.
The month in which the maximum number of students were born is August.
Example 2. A family with a monthly income of ₹ 20,000 had planned the following expenditures per month under various heads:
Table 12.1
| Heads | Expenditure (in thousand rupees) |
|---|---|
| Grocery | 4 |
| Rent | 5 |
| Education of children | 5 |
| Medicine | 2 |
| Fuel | 2 |
| Entertainment | 1 |
| Miscellaneous | 1 |
Draw a bar graph for the data above.
Answer:
Given:
Monthly income of a family = $\textsf{₹} 20,000$
Expenditure under various heads is provided in Table 12.1.
To Draw:
A bar graph for the given data.
Solution:
The given data is summarized in the table below:
| Heads | Expenditure (in thousand rupees) |
| Grocery | 4 |
| Rent | 5 |
| Education of children | 5 |
| Medicine | 2 |
| Fuel | 2 |
| Entertainment | 1 |
| Miscellaneous | 1 |
To draw the bar graph, we follow these steps:
1. Draw two perpendicular axes, the horizontal axis (x-axis) and the vertical axis (y-axis).
2. Mark the 'Heads' of expenditure (Grocery, Rent, Education of children, Medicine, Fuel, Entertainment, Miscellaneous) on the horizontal axis. Leave equal spacing between the marks for each head.
3. Mark the 'Expenditure (in thousand rupees)' on the vertical axis. Since the maximum expenditure is 5 thousand rupees, a suitable scale for the vertical axis would be 1 unit length representing 1 thousand rupees. We can mark points at 0, 1, 2, 3, 4, 5, etc., on the y-axis.
4. Draw bars of uniform width for each 'Head' on the horizontal axis. The height of each bar should correspond to the expenditure for that head, based on the chosen scale on the vertical axis.
- For Grocery, draw a bar of height 4 units.
- For Rent, draw a bar of height 5 units.
- For Education of children, draw a bar of height 5 units.
- For Medicine, draw a bar of height 2 units.
- For Fuel, draw a bar of height 2 units.
- For Entertainment, draw a bar of height 1 unit.
- For Miscellaneous, draw a bar of height 1 unit.
5. The bar graph should visually represent these heights.
The resulting bar graph will show the distribution of the family's monthly expenditure across different heads.
Example 3. A teacher wanted to analyse the performance of two sections of students in a mathematics test of 100 marks. Looking at their performances, she found that a few students got under 20 marks and a few got 70 marks or above. So she decided to group them into intervals of varying sizes as follows: 0 - 20, 20 - 30, . . ., 60 - 70, 70 - 100. Then she formed the following table:
Table 12.3
| Marks | Number of students |
|---|---|
| 0 - 20 | 7 |
| 20 - 30 | 10 |
| 30 - 40 | 10 |
| 40 - 50 | 20 |
| 50 - 60 | 20 |
| 60 - 70 | 15 |
| 70 - above | 8 |
| Total | 90 |
Draw a histogram corresponding to this frequency distribution table provided above.
Answer:
Given:
A frequency distribution table showing the marks obtained by 90 students in a mathematics test, grouped into intervals of varying sizes.
To Draw:
A histogram for the given frequency distribution table.
Solution:
The given frequency distribution has class intervals of unequal widths. To draw a histogram for such a distribution, the areas of the rectangles should be proportional to the frequencies. The area of a rectangle is given by width $\times$ height. Since the area must be proportional to the frequency, the height of each rectangle needs to be adjusted such that:
Height of the rectangle $\propto \frac{\text{Frequency of the class}}{\text{Width of the class}}$
We usually calculate the 'adjusted frequency' or 'height of the rectangle' using a standard width (the minimum class width) as a reference. The formula is:
Adjusted Frequency (Height) $= \frac{\text{Frequency of the class}}{\text{Width of the class}} \times \text{Minimum class width}$
From the table, the class intervals and their frequencies are:
| Marks (Class Interval) | Frequency (Number of students) | Width of the class |
| 0 - 20 | 7 | $20 - 0 = 20$ |
| 20 - 30 | 10 | $30 - 20 = 10$ |
| 30 - 40 | 10 | $40 - 30 = 10$ |
| 40 - 50 | 20 | $50 - 40 = 10$ |
| 50 - 60 | 20 | $60 - 50 = 10$ |
| 60 - 70 | 15 | $70 - 60 = 10$ |
| 70 - 100 | 8 | $100 - 70 = 30$ |
The minimum class width among these intervals is 10.
Now, we calculate the adjusted frequency for each class using the minimum width of 10:
1. For class [0, 20): Adjusted Frequency $= \frac{7}{20} \times 10 = \frac{7}{\cancel{20}_{2}} \times \cancel{10}^{1} = \frac{7}{2} = 3.5$
2. For class [20, 30): Adjusted Frequency $= \frac{10}{10} \times 10 = 10$
3. For class [30, 40): Adjusted Frequency $= \frac{10}{10} \times 10 = 10$
4. For class [40, 50): Adjusted Frequency $= \frac{20}{10} \times 10 = 20$
5. For class [50, 60): Adjusted Frequency $= \frac{20}{10} \times 10 = 20$
6. For class [60, 70): Adjusted Frequency $= \frac{15}{10} \times 10 = 15$
7. For class [70, 100): Adjusted Frequency $= \frac{8}{30} \times 10 = \frac{8}{\cancel{30}_{3}} \times \cancel{10}^{1} = \frac{8}{3}$ (approximately 2.67)
To draw the histogram:
1. Draw the horizontal axis and label it 'Marks'. Mark the points corresponding to the class boundaries: 0, 20, 30, 40, 50, 60, 70, 100.
2. Draw the vertical axis and label it 'Adjusted Frequency' or 'Height of the rectangle'. Choose a suitable scale for the adjusted frequencies (e.g., from 0 to 20, marking intervals of 2 or 5).
3. Draw rectangles over each class interval. The base of each rectangle should be the width of the class interval on the horizontal axis, and the height should be the corresponding adjusted frequency calculated above.
- For the interval [0, 20), draw a rectangle with height 3.5.
- For the interval [20, 30), draw a rectangle with height 10.
- For the interval [30, 40), draw a rectangle with height 10.
- For the interval [40, 50), draw a rectangle with height 20.
- For the interval [50, 60), draw a rectangle with height 20.
- For the interval [60, 70), draw a rectangle with height 15.
- For the interval [70, 100), draw a rectangle with height $\frac{8}{3}$ (approx. 2.67).
The rectangles should be adjacent.
Example 4. Consider the marks, out of 100, obtained by 51 students of a class in a test, given in Table 12.5.
Table 12.5
| Marks | Number of students |
|---|---|
| 0 - 10 | 5 |
| 10 - 20 | 10 |
| 20 - 30 | 4 |
| 30 - 40 | 6 |
| 40 - 50 | 7 |
| 50 - 60 | 3 |
| 60 - 70 | 2 |
| 70 - 80 | 2 |
| 80 - 90 | 3 |
| 90 - 100 | 9 |
| Total | 51 |
Draw a frequency polygon corresponding to this frequency distribution table.
Answer:
Given:
A frequency distribution table showing the marks obtained by 51 students in a test, grouped into equal class intervals of width 10.
To Draw:
A frequency polygon for the given data.
Solution:
To draw a frequency polygon from a frequency distribution table, we first need to find the class mark (or midpoint) of each class interval. The class mark is calculated using the formula:
Class Mark $= \frac{\text{Lower limit} + \text{Upper limit}}{2}$
We will then plot points on a graph. The x-coordinate of each point will be the class mark, and the y-coordinate will be the frequency of that class.
Let's calculate the class marks for the given data and list the points:
| Marks (Class Interval) | Frequency (Number of students) | Class Mark | Point (Class Mark, Frequency) |
| 0 - 10 | 5 | $\frac{0+10}{2} = 5$ | (5, 5) |
| 10 - 20 | 10 | $\frac{10+20}{2} = 15$ | (15, 10) |
| 20 - 30 | 4 | $\frac{20+30}{2} = 25$ | (25, 4) |
| 30 - 40 | 6 | $\frac{30+40}{2} = 35$ | (35, 6) |
| 40 - 50 | 7 | $\frac{40+50}{2} = 45$ | (45, 7) |
| 50 - 60 | 3 | $\frac{50+60}{2} = 55$ | (55, 3) |
| 60 - 70 | 2 | $\frac{60+70}{2} = 65$ | (65, 2) |
| 70 - 80 | 2 | $\frac{70+80}{2} = 75$ | (75, 2) |
| 80 - 90 | 3 | $\frac{80+90}{2} = 85$ | (85, 3) |
| 90 - 100 | 9 | $\frac{90+100}{2} = 95$ | (95, 9) |
To make the frequency polygon a closed figure and bring it down to the horizontal axis, we consider two imaginary class intervals:
1. An interval before the first interval [0, 10). Since the class width is 10, this imaginary interval would be [-10, 0). Its class mark is $\frac{-10+0}{2} = -5$. We assume its frequency is 0. This gives the point (-5, 0).
2. An interval after the last interval [90, 100]. This imaginary interval would be [100, 110). Its class mark is $\frac{100+110}{2} = 105$. We assume its frequency is 0. This gives the point (105, 0).
The points we need to plot on the graph are: (-5, 0), (5, 5), (15, 10), (25, 4), (35, 6), (45, 7), (55, 3), (65, 2), (75, 2), (85, 3), (95, 9), and (105, 0).
Now, let's draw the frequency polygon:
1. Draw the horizontal axis (x-axis) and label it 'Marks'. Mark the class marks at equal distances along this axis, starting from -5 and going up to 105 (e.g., -5, 5, 15, 25, ... 105).
2. Draw the vertical axis (y-axis) and label it 'Number of students' or 'Frequency'. Choose a suitable scale for the frequency based on the values (0 to 10). For example, 1 unit on the y-axis can represent 1 student.
3. Plot the points we identified: (-5, 0), (5, 5), (15, 10), (25, 4), (35, 6), (45, 7), (55, 3), (65, 2), (75, 2), (85, 3), (95, 9), and (105, 0).
4. Connect these plotted points with straight line segments in order from left to right. The resulting closed figure is the frequency polygon.
Example 5. In a city, the weekly observations made in a study on the cost of living index are given in the following table:
Table 12.6
| Cost of living index | Number of weeks |
|---|---|
| 140 - 150 | 5 |
| 150 - 160 | 10 |
| 160 - 170 | 20 |
| 170 - 180 | 9 |
| 180 - 190 | 6 |
| 190 - 200 | 2 |
| Total | 52 |
Draw a frequency polygon corresponding to this frequency distribution table.
Answer:
Given:
A frequency distribution table showing the weekly observations on the cost of living index and the corresponding number of weeks:
| Cost of living index | Number of weeks |
| 140 - 150 | 5 |
| 150 - 160 | 10 |
| 160 - 170 | 20 |
| 170 - 180 | 9 |
| 180 - 190 | 6 |
| 190 - 200 | 2 |
| Total | 52 |
To Draw:
A frequency polygon for the given data.
Solution:
To draw a frequency polygon, we need to find the class mark (midpoint) of each class interval. The class mark is calculated using the formula:
Class Mark $= \frac{\text{Lower limit} + \text{Upper limit}}{2}$
We will then plot points on a graph. The x-coordinate of each point will be the class mark, and the y-coordinate will be the frequency of that class.
Let's calculate the class marks for the given data and list the points:
| Cost of living index (Class Interval) | Number of weeks (Frequency) | Class Mark | Point (Class Mark, Frequency) |
| 140 - 150 | 5 | $\frac{140+150}{2} = 145$ | (145, 5) |
| 150 - 160 | 10 | $\frac{150+160}{2} = 155$ | (155, 10) |
| 160 - 170 | 20 | $\frac{160+170}{2} = 165$ | (165, 20) |
| 170 - 180 | 9 | $\frac{170+180}{2} = 175$ | (175, 9) |
| 180 - 190 | 6 | $\frac{180+190}{2} = 185$ | (185, 6) |
| 190 - 200 | 2 | $\frac{190+200}{2} = 195$ | (195, 2) |
The class width is 10 (e.g., $150 - 140 = 10$).
To make the frequency polygon a closed figure and bring it down to the horizontal axis, we consider two imaginary class intervals:
1. An interval before the first interval [140, 150). Since the class width is 10, this imaginary interval would be [130, 140). Its class mark is $\frac{130+140}{2} = 135$. We assume its frequency is 0. This gives the point (135, 0).
2. An interval after the last interval [190, 200). This imaginary interval would be [200, 210). Its class mark is $\frac{200+210}{2} = 205$. We assume its frequency is 0. This gives the point (205, 0).
The points we need to plot on the graph are: (135, 0), (145, 5), (155, 10), (165, 20), (175, 9), (185, 6), (195, 2), and (205, 0).
Now, let's draw the frequency polygon:
1. Draw the horizontal axis (x-axis) and label it 'Cost of living index'. Mark the class marks at equal distances along this axis, starting from 135 and going up to 205 (e.g., 135, 145, 155, ... 205).
2. Draw the vertical axis (y-axis) and label it 'Number of weeks' or 'Frequency'. Choose a suitable scale for the frequency based on the values (0 to 20). For example, 1 unit on the y-axis can represent 2 weeks.
3. Plot the points we identified: (135, 0), (145, 5), (155, 10), (165, 20), (175, 9), (185, 6), (195, 2), and (205, 0).
4. Connect these plotted points with straight line segments in order from left to right. The resulting closed figure is the frequency polygon.
Exercise 12.1
Question 1. A survey conducted by an organisation for the cause of illness and death among the women between the ages 15 - 44 (in years) worldwide, found the following figures (in %):
| S.No. | Causes | Female fatality rate (%) |
|---|---|---|
| 1. | Reproductive health conditions | 31.8 |
| 2. | Neuropsychiatric conditions | 25.4 |
| 3. | Injuries | 12.4 |
| 4. | Cardiovascular conditions | 4.3 |
| 5. | Respiratory conditions | 4.1 |
| 6. | Other causes | 22.0 |
(i) Represent the information given above graphically.
(ii) Which condition is the major cause of women’s ill health and death worldwide?
(iii) Try to find out, with the help of your teacher, any two factors which play a major role in the cause in (ii) above being the major cause.
Answer:
Given:
Data showing the percentage of female fatality rate for different causes among women aged 15-44 worldwide.
| S.No. | Causes | Female fatality rate (%) |
| 1. | Reproductive health conditions | 31.8 |
| 2. | Neuropsychiatric conditions | 25.4 |
| 3. | Injuries | 12.4 |
| 4. | Cardiovascular conditions | 4.3 |
| 5. | Respiratory conditions | 4.1 |
| 6. | Other causes | 22.0 |
To Find:
(i) Graphical representation of the data.
(ii) The major cause of women's ill health and death worldwide.
(iii) Two factors contributing to the major cause (requires external knowledge).
Solution:
Part (i): Graphical representation
The given data represents the fatality rate for different categories of causes. This type of data is best represented using a bar graph.
To draw the bar graph, follow these steps:
1. Draw two perpendicular axes. The horizontal axis (x-axis) will represent the 'Causes', and the vertical axis (y-axis) will represent the 'Female fatality rate (%)'.
2. Mark the different causes (Reproductive health conditions, Neuropsychiatric conditions, Injuries, etc.) along the horizontal axis. Leave equal space between the bars.
3. Choose a suitable scale for the vertical axis. The fatality rates range from 4.1% to 31.8%. A scale from 0% to 35% or 40% with intervals of 5% would be appropriate.
4. Draw bars of uniform width for each cause. The height of each bar should correspond to the percentage given in the table, according to the scale chosen on the vertical axis.
- For 'Reproductive health conditions', draw a bar up to the level of 31.8%.
- For 'Neuropsychiatric conditions', draw a bar up to the level of 25.4%.
- For 'Injuries', draw a bar up to the level of 12.4%.
- For 'Cardiovascular conditions', draw a bar up to the level of 4.3%.
- For 'Respiratory conditions', draw a bar up to the level of 4.1%.
- For 'Other causes', draw a bar up to the level of 22.0%.
Label both axes clearly. The bar graph will visually compare the fatality rates of different causes.
Part (ii): Major cause of women’s ill health and death worldwide
To find the major cause from the given data, we need to identify the cause with the highest female fatality rate percentage.
Looking at the 'Female fatality rate (%)' column in the table:
Reproductive health conditions: 31.8%
Neuropsychiatric conditions: 25.4%
Injuries: 12.4%
Cardiovascular conditions: 4.3%
Respiratory conditions: 4.1%
Other causes: 22.0%
The highest percentage among these is 31.8%.
This highest percentage corresponds to Reproductive health conditions.
Therefore, the major cause of women’s ill health and death worldwide, according to this survey, is Reproductive health conditions.
Part (iii): Factors contributing to the major cause
The major cause identified in Part (ii) is 'Reproductive health conditions'. Several factors can contribute to this being a leading cause of ill health and death among women, especially in certain parts of the world. As suggested in the question, discuss this with your teacher to understand the specific factors.
However, some general factors that contribute to poor reproductive health outcomes can include:
1. Lack of access to quality healthcare: Many women, particularly in developing regions, may not have access to necessary medical services like prenatal care, skilled birth attendants, emergency obstetric care, and family planning services. This can lead to complications during pregnancy and childbirth, unsafe abortions, and untreated infections.
2. Socio-economic factors: Poverty, lack of education, malnutrition, and poor sanitation can all negatively impact reproductive health. Early marriages, frequent pregnancies, and inadequate spacing between children also put women's bodies under stress and increase risks.
These factors often interact with each other, making it harder for women to maintain good reproductive health.
Question 2. The following data on the number of girls (to the nearest ten) per thousand boys in different sections of Indian society is given below.
| Section | Number of girls per thousand boys |
|---|---|
| Scheduled Caste (SC) | 940 |
| Scheduled Tribe (SC) | 970 |
| Non SC/ST | 920 |
| Backward districts | 950 |
| Non - backward districts | 920 |
| Rural | 930 |
| Urban | 910 |
(i) Represent the information above by a bar graph.
(ii) In the classroom discuss what conclusions can be arrived at from the graph.
Answer:
Given:
Data on the number of girls (to the nearest ten) per thousand boys in different sections of Indian society.
| Section | Number of girls per thousand boys |
| Scheduled Caste (SC) | 940 |
| Scheduled Tribe (ST) | 970 |
| Non SC/ST | 920 |
| Backward districts | 950 |
| Non - backward districts | 920 |
| Rural | 930 |
| Urban | 910 |
To Do:
(i) Represent the information by a bar graph.
(ii) Discuss conclusions from the graph.
Solution:
Part (i): Bar Graph Representation
To represent the information by a bar graph, we follow these steps:
1. Draw two perpendicular axes, the horizontal axis (x-axis) and the vertical axis (y-axis).
2. Mark the 'Section' (Scheduled Caste (SC), Scheduled Tribe (ST), Non SC/ST, Backward districts, Non - backward districts, Rural, Urban) on the horizontal axis. Leave equal spacing between the marks for each section.
3. Mark the 'Number of girls per thousand boys' on the vertical axis. The values range from 910 to 970. We can use a scale that starts from a value close to these numbers, like 900, and goes up to a value slightly above the maximum, like 980 or 1000. Since the range of values is relatively small compared to starting from 0, it might be helpful to use a break (represented by a zig-zag line) on the y-axis near the origin (0) and start the scale from 900 to show the variations clearly. Let's use a scale starting from 900 with increments of 10.
4. Draw bars of uniform width for each section. The base of each bar will be centered on the mark for the section on the horizontal axis, and the height of the bar will represent the corresponding number of girls per thousand boys according to the scale on the vertical axis.
- For Scheduled Caste (SC), draw a bar up to 940.
- For Scheduled Tribe (ST), draw a bar up to 970.
- For Non SC/ST, draw a bar up to 920.
- For Backward districts, draw a bar up to 950.
- For Non - backward districts, draw a bar up to 920.
- For Rural, draw a bar up to 930.
- For Urban, draw a bar up to 910.
5. Label the axes clearly as 'Section' on the x-axis and 'Number of girls per thousand boys' on the y-axis. Give a suitable title to the bar graph, for example, 'Number of Girls per Thousand Boys in Different Sections of Indian Society'.
The resulting bar graph will visually represent the number of girls per thousand boys for each section, making it easy to compare them.
Part (ii): Conclusions from the graph (Discussion Points)
By looking at the heights of the bars in the bar graph (or by comparing the numbers in the table), we can draw several conclusions about the sex ratio in different sections of Indian society. These conclusions can be discussed in the classroom:
1. Gender Imbalance: The most evident conclusion is that in all the listed sections of Indian society, the number of girls per thousand boys is less than 1000. This indicates that there are fewer girls compared to boys, which points towards a significant gender imbalance.
2. Highest Ratio: The bar for the Scheduled Tribe (ST) section is the tallest, showing the highest ratio of girls per thousand boys (970) among all the categories listed.
3. Lowest Ratio: The bar for the Urban section is the shortest, indicating the lowest ratio of girls per thousand boys (910). The Non SC/ST and Non-backward districts sections also have a relatively low ratio (both 920).
4. Rural vs. Urban: The sex ratio is higher in Rural areas (930) compared to Urban areas (910).
5. Scheduled Caste/Tribe vs. Non-SC/ST: The sex ratio in SC (940) and ST (970) categories is generally higher than in the Non SC/ST category (920).
6. Backward vs. Non-backward Districts: Backward districts (950) have a higher sex ratio than Non-backward districts (920).
7. Need for Awareness: The overall trend of less than 1000 girls per thousand boys suggests societal issues like preference for male children, potentially leading to practices that affect the girl child. This highlights the need for social awareness campaigns and efforts to promote gender equality and the value of the girl child.
These points can be discussed to understand the social implications of these statistics and the reasons behind the observed differences between different sections.
Question 3. Given below are the seats won by different political parties in the polling outcome of a state assembly elections:
| Political Party | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| Seats Won | 75 | 55 | 37 | 29 | 10 | 37 |
(i) Draw a bar graph to represent the polling results.
(ii) Which political party won the maximum number of seats?
Answer:
Given:
The number of seats won by different political parties (A, B, C, D, E, F) in a state assembly election.
| Political Party | A | B | C | D | E | F |
| Seats Won | 75 | 55 | 37 | 29 | 10 | 37 |
To Do:
(i) Draw a bar graph to represent the polling results.
(ii) Which political party won the maximum number of seats?
Solution:
Part (i): Bar Graph Representation
To represent the given data using a bar graph, we will follow these steps:
1. Draw two perpendicular lines. The horizontal line is called the x-axis, and the vertical line is called the y-axis. The point where they meet is the origin (0).
2. On the horizontal axis (x-axis), we will represent the 'Political Party'. We will mark points for each party (A, B, C, D, E, F) at equal distances from each other.
3. On the vertical axis (y-axis), we will represent the 'Number of Seats Won'. We need to choose a scale for the y-axis. The number of seats ranges from 10 to 75. A suitable scale would be to let 1 unit length on the y-axis represent 10 seats. So, we can mark points at 0, 10, 20, 30, 40, 50, 60, 70, 80, etc., on the y-axis.
4. Now, draw bars of uniform width above the marks for each political party on the x-axis. The height of each bar should correspond to the number of seats won by that party, according to the scale on the y-axis.
- For Political Party A, draw a bar up to the height corresponding to 75 on the y-axis.
- For Political Party B, draw a bar up to the height corresponding to 55.
- For Political Party C, draw a bar up to the height corresponding to 37. (This will be between 30 and 40).
- For Political Party D, draw a bar up to the height corresponding to 29. (This will be just below 30).
- For Political Party E, draw a bar up to the height corresponding to 10.
- For Political Party F, draw a bar up to the height corresponding to 37. (Same height as Party C).
5. Label the horizontal axis as 'Political Party' and the vertical axis as 'Seats Won'. Give a title to the graph, such as 'Seats Won by Political Parties'.
The bar graph will visually show the number of seats won by each party, making it easy to compare their performance.
Part (ii): Political party that won the maximum number of seats
To find which political party won the maximum number of seats, we look at the table or the bar graph and find the highest number of seats won.
From the table:
Party A: 75 seats
Party B: 55 seats
Party C: 37 seats
Party D: 29 seats
Party E: 10 seats
Party F: 37 seats
Comparing these numbers, the highest number is 75.
This corresponds to Political Party A.
Also, in the bar graph, the tallest bar is the one for Party A.
Therefore, the political party that won the maximum number of seats is Party A.
Question 4. The length of 40 leaves of a plant are measured correct to one millimetre, and the obtained data is represented in the following table:
| Length (in mm) | Number of leaves |
|---|---|
| 118 - 126 | 3 |
| 127 - 135 | 5 |
| 136 - 144 | 9 |
| 145 - 153 | 12 |
| 154 - 162 | 5 |
| 163 - 171 | 4 |
| 172 - 180 | 2 |
(i) Draw a histogram to represent the given data. [Hint: First make the class intervals continuous]
(ii) Is there any other suitable graphical representation for the same data?
(iii) Is it correct to conclude that the maximum number of leaves are 153 mm long? Why?
Answer:
Given:
A frequency distribution table showing the length of 40 leaves measured correct to one millimetre.
| Length (in mm) | Number of leaves |
| 118 - 126 | 3 |
| 127 - 135 | 5 |
| 136 - 144 | 9 |
| 145 - 153 | 12 |
| 154 - 162 | 5 |
| 163 - 171 | 4 |
| 172 - 180 | 2 |
To Do:
(i) Draw a histogram to represent the given data.
(ii) Determine if there is any other suitable graphical representation for the same data.
(iii) Determine if it is correct to conclude that the maximum number of leaves are 153 mm long and explain why.
Solution:
Part (i): Draw a histogram
A histogram is used for continuous class intervals. The given class intervals (118-126, 127-135, etc.) are discontinuous because there is a gap of 1 mm between the upper limit of one class and the lower limit of the next class (e.g., 127 - 126 = 1).
To make the class intervals continuous, we need to adjust the boundaries. We find half the difference between the upper limit of a class and the lower limit of the next class. The difference is 1, so half the difference is $\frac{1}{2} = 0.5$ mm.
We subtract 0.5 from the lower limit of each class and add 0.5 to the upper limit of each class.
The adjusted (continuous) class intervals and their frequencies are:
| Continuous Length (in mm) | Number of leaves (Frequency) |
| 118 - 0.5 to 126 + 0.5 = 117.5 - 126.5 | 3 |
| 127 - 0.5 to 135 + 0.5 = 126.5 - 135.5 | 5 |
| 136 - 0.5 to 144 + 0.5 = 135.5 - 144.5 | 9 |
| 145 - 0.5 to 153 + 0.5 = 144.5 - 153.5 | 12 |
| 154 - 0.5 to 162 + 0.5 = 153.5 - 162.5 | 5 |
| 163 - 0.5 to 171 + 0.5 = 162.5 - 171.5 | 4 |
| 172 - 0.5 to 180 + 0.5 = 171.5 - 180.5 | 2 |
Now, all class intervals are continuous, and the width of each class is $126.5 - 117.5 = 9$, $135.5 - 126.5 = 9$, and so on. All continuous class intervals have an equal width of 9 mm.
To draw the histogram:
1. Draw the horizontal axis (x-axis) and label it 'Length (in mm)'. Mark the continuous class boundaries (117.5, 126.5, 135.5, 144.5, 153.5, 162.5, 171.5, 180.5) at equal distances.
2. Draw the vertical axis (y-axis) and label it 'Number of leaves' or 'Frequency'. Choose a suitable scale for the frequency. Since the maximum frequency is 12, a scale from 0 to 14 with increments of 2 would be appropriate.
3. Draw rectangles over each class interval. The base of each rectangle is the width of the continuous class interval on the x-axis (e.g., from 117.5 to 126.5), and the height is equal to the corresponding frequency (number of leaves).
- Draw a rectangle from 117.5 to 126.5 with height 3.
- Draw a rectangle from 126.5 to 135.5 with height 5.
- Draw a rectangle from 135.5 to 144.5 with height 9.
- Draw a rectangle from 144.5 to 153.5 with height 12.
- Draw a rectangle from 153.5 to 162.5 with height 5.
- Draw a rectangle from 162.5 to 171.5 with height 4.
- Draw a rectangle from 171.5 to 180.5 with height 2.
The rectangles in the histogram will be adjacent to each other.
Part (ii): Other suitable graphical representation
Yes, besides a histogram, another suitable graphical representation for this type of grouped frequency data is a Frequency Polygon.
A frequency polygon can be drawn by plotting points corresponding to the class mark (midpoint) of each continuous class interval against its frequency, and then joining these points with line segments. You would also connect the first and last points to the midpoints of the imaginary classes before and after the data range on the x-axis to form a closed polygon.
Part (iii): Conclusion about leaves being 153 mm long
No, it is not correct to conclude that the maximum number of leaves are exactly 153 mm long.
Here's why:
1. Grouped Data: The data is presented in grouped form. The class interval 145 - 153 mm (or 144.5 - 153.5 mm continuously) tells us that there are 12 leaves whose lengths fall within this range. It does not give us the exact length of each individual leaf within that group.
2. Class Interval vs. Single Value: The histogram (or table) shows that the class with the highest frequency (12 leaves) is the one covering the length range from 144.5 mm to 153.5 mm. This means that more leaves have lengths somewhere between 144.5 mm and 153.5 mm than in any other 9 mm range, but we don't know if any of them is precisely 153 mm, or if 153 mm is the most frequent length.
3. Correct Conclusion: The correct conclusion is that the class interval 144.5 - 153.5 mm contains the maximum number of leaves (12 leaves). We cannot pinpoint a single length within a class interval as the most frequent length from a grouped frequency distribution table.
Question 5. The following table gives the life times of 400 neon lamps:
| Life time (in hours) | Number of lamps |
|---|---|
| 300 - 400 | 14 |
| 400 - 500 | 56 |
| 500 - 600 | 60 |
| 600 - 700 | 86 |
| 700 - 800 | 74 |
| 800 - 900 | 62 |
| 900 - 1000 | 48 |
(i) Represent the given information with the help of a histogram.
(ii) How many lamps have a life time of more than 700 hours?
Answer:
Given:
A frequency distribution table showing the life times of 400 neon lamps.
| Life time (in hours) | Number of lamps |
| 300 - 400 | 14 |
| 400 - 500 | 56 |
| 500 - 600 | 60 |
| 600 - 700 | 86 |
| 700 - 800 | 74 |
| 800 - 900 | 62 |
| 900 - 1000 | 48 |
To Do:
(i) Represent the given information with the help of a histogram.
(ii) Find the number of lamps that have a life time of more than 700 hours.
Solution:
Part (i): Histogram representation
A histogram is used to represent continuous grouped data. In the given table, the class intervals for 'Life time (in hours)' are already continuous (the upper limit of one class is the same as the lower limit of the next class, e.g., 400, 500, 600, etc.). Also, the width of each class interval is the same:
$400 - 300 = 100$ hours
$500 - 400 = 100$ hours
... and so on, up to
$1000 - 900 = 100$ hours
Since the class intervals are continuous and have equal width, the height of each rectangle in the histogram will be equal to the frequency (number of lamps) in that class.
To draw the histogram:
1. Draw two perpendicular axes. The horizontal axis (x-axis) will represent the 'Life time (in hours)', and the vertical axis (y-axis) will represent the 'Number of lamps' (frequency).
2. Mark the class boundaries (300, 400, 500, 600, 700, 800, 900, 1000) on the horizontal axis at equal distances.
3. Choose a suitable scale for the vertical axis to represent the number of lamps. The frequencies range from 14 to 86. A scale starting from 0 and going up to 90 or 100 with intervals of 10 would be appropriate (e.g., 1 unit length = 10 lamps).
4. Draw rectangles with the class intervals as bases on the horizontal axis and heights equal to the corresponding frequencies from the table.
- Draw a rectangle from 300 to 400 on the x-axis with a height of 14 on the y-axis.
- Draw a rectangle from 400 to 500 with a height of 56.
- Draw a rectangle from 500 to 600 with a height of 60.
- Draw a rectangle from 600 to 700 with a height of 86.
- Draw a rectangle from 700 to 800 with a height of 74.
- Draw a rectangle from 800 to 900 with a height of 62.
- Draw a rectangle from 900 to 1000 with a height of 48.
The rectangles in the histogram will be adjacent to each other, showing the continuous nature of the data.
Part (ii): Number of lamps with life time more than 700 hours
We need to find the total number of lamps whose life time is greater than 700 hours. Looking at the table, these are the lamps in the following class intervals:
- 700 - 800 hours
- 800 - 900 hours
- 900 - 1000 hours
The number of lamps in each of these intervals are given in the 'Number of lamps' column:
- For 700 - 800 hours: 74 lamps
- For 800 - 900 hours: 62 lamps
- For 900 - 1000 hours: 48 lamps
To find the total number of lamps with a life time of more than 700 hours, we add the number of lamps in these intervals:
Total number of lamps $> 700$ hours $= (\text{Lamps in 700-800}) + (\text{Lamps in 800-900}) + (\text{Lamps in 900-1000})$
Total number $= 74 + 62 + 48$
Let's add these numbers:
$74 + 62 = 136$
$136 + 48 = 184$
So, the total number of lamps with a life time of more than 700 hours is 184.
The number of lamps that have a life time of more than 700 hours is 184.
Question 6. The following table gives the distribution of students of two sections according to the marks obtained by them:
| Section A | Section B | ||
| Marks | Frequency | Marks | Frequency |
| 0 - 10 | 3 | 0 - 10 | 5 |
| 10 - 20 | 9 | 10 - 20 | 19 |
| 20 - 30 | 17 | 20 - 30 | 15 |
| 30 - 40 | 12 | 30 - 40 | 10 |
| 40 - 50 | 9 | 40 - 50 | 1 |
Represent the marks of the students of both the sections on the same graph by two frequency polygons. From the two polygons compare the performance of the two sections.
Answer:
Given:
Frequency distribution of marks obtained by students of two sections (Section A and Section B) in a test, given in a table.
| Section A | Section B | ||
| Marks | Frequency | Marks | Frequency |
| 0 - 10 | 3 | 0 - 10 | 5 |
| 10 - 20 | 9 | 10 - 20 | 19 |
| 20 - 30 | 17 | 20 - 30 | 15 |
| 30 - 40 | 12 | 30 - 40 | 10 |
| 40 - 50 | 9 | 40 - 50 | 1 |
To Do:
(i) Represent the marks of both sections on the same graph using two frequency polygons.
(ii) Compare the performance of the two sections from the polygons.
Solution:
Part (i): Frequency Polygons
To draw a frequency polygon, we need to find the class mark (midpoint) of each class interval. The class intervals are continuous and have equal width of $10 - 0 = 10$.
The formula for Class Mark is:
Class Mark $= \frac{\text{Lower limit} + \text{Upper limit}}{2}$
Let's calculate the class marks for the given intervals:
- For class 0 - 10: Class Mark $= \frac{0+10}{2} = 5$
- For class 10 - 20: Class Mark $= \frac{10+20}{2} = 15$
- For class 20 - 30: Class Mark $= \frac{20+30}{2} = 25$
- For class 30 - 40: Class Mark $= \frac{30+40}{2} = 35$
- For class 40 - 50: Class Mark $= \frac{40+50}{2} = 45$
To make the frequency polygons closed figures, we need to include the class marks of hypothetical class intervals immediately before the first class and immediately after the last class, each with a frequency of 0. Since the class width is 10:
The class before 0 - 10 is -10 to 0. Its class mark is $\frac{-10+0}{2} = -5$. Frequency is 0.
The class after 40 - 50 is 50 to 60. Its class mark is $\frac{50+60}{2} = 55$. Frequency is 0.
Now we have the points (Class Mark, Frequency) for both sections:
| Class Mark | Frequency (Section A) | Point for Section A | Frequency (Section B) | Point for Section B |
| -5 | 0 | (-5, 0) | 0 | (-5, 0) |
| 5 | 3 | (5, 3) | 5 | (5, 5) |
| 15 | 9 | (15, 9) | 19 | (15, 19) |
| 25 | 17 | (25, 17) | 15 | (25, 15) |
| 35 | 12 | (35, 12) | 10 | (35, 10) |
| 45 | 9 | (45, 9) | 1 | (45, 1) |
| 55 | 0 | (55, 0) | 0 | (55, 0) |
To draw the frequency polygons on the same graph:
1. Draw the horizontal axis (x-axis) and label it 'Marks'. Mark the class marks (-5, 5, 15, 25, 35, 45, 55) at equal intervals.
2. Draw the vertical axis (y-axis) and label it 'Frequency' (Number of students). Choose a suitable scale for the frequency. Since the maximum frequency is 19, a scale from 0 to 20 or 25 with increments of 2 or 5 would be appropriate.
3. Plot the points for Section A: (-5, 0), (5, 3), (15, 9), (25, 17), (35, 12), (45, 9), (55, 0). Connect these points with straight line segments. Use one colour or line style for Section A.
4. Plot the points for Section B: (-5, 0), (5, 5), (15, 19), (25, 15), (35, 10), (45, 1), (55, 0) on the same graph. Connect these points with straight line segments. Use a different colour or line style for Section B.
5. Provide a key or legend to distinguish between the frequency polygon for Section A and Section B.
Part (ii): Comparison of performance
By examining the two frequency polygons on the same graph, we can compare the performance of the two sections:
1. Peak of the Graph: The peak of a frequency polygon indicates the class interval where the maximum number of students scored marks. For Section A, the peak is at the class mark 25 (20-30 marks), with 17 students. For Section B, the peak is at the class mark 15 (10-20 marks), with 19 students.
2. Distribution of Marks:
- Section B has a higher concentration of students in the lower marks range (especially 10-20 marks).
- Section A has a higher concentration of students in the middle to higher marks ranges (20-30, 30-40, and 40-50 marks). Notice that the frequencies for Section A are higher than Section B in the 20-30, 30-40, and 40-50 ranges.
3. Overall Performance: Since a larger proportion of students in Section A scored higher marks compared to Section B (where many students are concentrated in the 10-20 range and very few in the 40-50 range), it indicates that Section A performed better overall in the test than Section B.
The frequency polygon for Section A is generally shifted towards the right side of the graph compared to Section B's polygon, visually representing that students in Section A tend to score higher marks.
Question 7. The runs scored by two teams A and B on the first 60 balls in a cricket match are given below:
| Number of balls | Team A | Team B |
|---|---|---|
| 1 - 6 | 2 | 5 |
| 7 - 12 | 1 | 6 |
| 13 - 18 | 8 | 2 |
| 19 - 24 | 9 | 10 |
| 25 - 30 | 4 | 5 |
| 31 - 36 | 5 | 6 |
| 37 - 42 | 6 | 3 |
| 43 - 48 | 10 | 4 |
| 49 - 54 | 6 | 8 |
| 55 - 60 | 2 | 10 |
Represent the data of both the teams on the same graph by frequency polygons.
[Hint: First make the class intervals continuous.]
Answer:
Given:
Runs scored by two cricket teams, Team A and Team B, in intervals of 6 balls for the first 60 balls.
| Number of balls | Team A (Runs) | Team B (Runs) |
| 1 - 6 | 2 | 5 |
| 7 - 12 | 1 | 6 |
| 13 - 18 | 8 | 2 |
| 19 - 24 | 9 | 10 |
| 25 - 30 | 4 | 5 |
| 31 - 36 | 5 | 6 |
| 37 - 42 | 6 | 3 |
| 43 - 48 | 10 | 4 |
| 49 - 54 | 6 | 8 |
| 55 - 60 | 2 | 10 |
To Draw:
Frequency polygons for Team A and Team B on the same graph.
Solution:
To draw frequency polygons, we need to use continuous class intervals and their corresponding class marks (midpoints).
The given class intervals (1-6, 7-12, etc.) are discontinuous. The difference between the upper limit of one class and the lower limit of the next class is $7 - 6 = 1$, $13 - 12 = 1$, and so on. The difference is 1.
To make the intervals continuous, we adjust the limits by subtracting $\frac{1}{2}$ of the difference (which is 0.5) from the lower limits and adding 0.5 to the upper limits.
The continuous class intervals are:
- 1 - 0.5 to 6 + 0.5 = 0.5 - 6.5
- 7 - 0.5 to 12 + 0.5 = 6.5 - 12.5
- 13 - 0.5 to 18 + 0.5 = 12.5 - 18.5
- 19 - 0.5 to 24 + 0.5 = 18.5 - 24.5
- 25 - 0.5 to 30 + 0.5 = 24.5 - 30.5
- 31 - 0.5 to 36 + 0.5 = 30.5 - 36.5
- 37 - 0.5 to 42 + 0.5 = 36.5 - 42.5
- 43 - 0.5 to 48 + 0.5 = 42.5 - 48.5
- 49 - 0.5 to 54 + 0.5 = 48.5 - 54.5
- 55 - 0.5 to 60 + 0.5 = 54.5 - 60.5
The class width is $6.5 - 0.5 = 6$.
Now, we find the class mark (midpoint) of each continuous class interval. The formula for Class Mark is:
Class Mark $= \frac{\text{Lower limit} + \text{Upper limit}}{2}$
- For interval 0.5 - 6.5: Class Mark $= \frac{0.5+6.5}{2} = \frac{7}{2} = 3.5$
- For interval 6.5 - 12.5: Class Mark $= \frac{6.5+12.5}{2} = \frac{19}{2} = 9.5$
- For interval 12.5 - 18.5: Class Mark $= \frac{12.5+18.5}{2} = \frac{31}{2} = 15.5$
- For interval 18.5 - 24.5: Class Mark $= \frac{18.5+24.5}{2} = \frac{43}{2} = 21.5$
- For interval 24.5 - 30.5: Class Mark $= \frac{24.5+30.5}{2} = \frac{55}{2} = 27.5$
- For interval 30.5 - 36.5: Class Mark $= \frac{30.5+36.5}{2} = \frac{67}{2} = 33.5$
- For interval 36.5 - 42.5: Class Mark $= \frac{36.5+42.5}{2} = \frac{79}{2} = 39.5$
- For interval 42.5 - 48.5: Class Mark $= \frac{42.5+48.5}{2} = \frac{91}{2} = 45.5$
- For interval 48.5 - 54.5: Class Mark $= \frac{48.5+54.5}{2} = \frac{103}{2} = 51.5$
- For interval 54.5 - 60.5: Class Mark $= \frac{54.5+60.5}{2} = \frac{115}{2} = 57.5$
To make the frequency polygons closed, we add hypothetical class intervals with zero frequency at the beginning and end. The class width is 6.
Imaginary class before 0.5 - 6.5: It would be from $0.5 - 6 = -5.5$ to 0.5. Class Mark $= \frac{-5.5+0.5}{2} = -2.5$. Frequency (Runs) = 0.
Imaginary class after 54.5 - 60.5: It would be from 60.5 to $60.5 + 6 = 66.5$. Class Mark $= \frac{60.5+66.5}{2} = \frac{127}{2} = 63.5$. Frequency (Runs) = 0.
The points (Class Mark, Runs) to be plotted for each team are:
| Class Mark (Number of balls) | Runs (Team A) | Point for Team A | Runs (Team B) | Point for Team B |
| -2.5 | 0 | (-2.5, 0) | 0 | (-2.5, 0) |
| 3.5 | 2 | (3.5, 2) | 5 | (3.5, 5) |
| 9.5 | 1 | (9.5, 1) | 6 | (9.5, 6) |
| 15.5 | 8 | (15.5, 8) | 2 | (15.5, 2) |
| 21.5 | 9 | (21.5, 9) | 10 | (21.5, 10) |
| 27.5 | 4 | (27.5, 4) | 5 | (27.5, 5) |
| 33.5 | 5 | (33.5, 5) | 6 | (33.5, 6) |
| 39.5 | 6 | (39.5, 6) | 3 | (39.5, 3) |
| 45.5 | 10 | (45.5, 10) | 4 | (45.5, 4) |
| 51.5 | 6 | (51.5, 6) | 8 | (51.5, 8) |
| 57.5 | 2 | (57.5, 2) | 10 | (57.5, 10) |
| 63.5 | 0 | (63.5, 0) | 0 | (63.5, 0) |
To draw the frequency polygons on the same graph:
1. Draw the horizontal axis (x-axis) and label it 'Number of balls (Class Mark)'. Mark the class marks (-2.5, 3.5, 9.5, ..., 63.5) at equal intervals.
2. Draw the vertical axis (y-axis) and label it 'Runs scored'. Choose a suitable scale for the number of runs (frequency). Since the maximum frequency is 10, a scale from 0 to 12 with increments of 2 would be appropriate.
3. Plot the points for Team A using one specific colour or line style (e.g., solid line): (-2.5, 0), (3.5, 2), (9.5, 1), (15.5, 8), (21.5, 9), (27.5, 4), (33.5, 5), (39.5, 6), (45.5, 10), (51.5, 6), (57.5, 2), (63.5, 0). Connect these points with straight line segments.
4. Plot the points for Team B using a different colour or line style (e.g., dashed line) on the same graph: (-2.5, 0), (3.5, 5), (9.5, 6), (15.5, 2), (21.5, 10), (27.5, 5), (33.5, 6), (39.5, 3), (45.5, 4), (51.5, 8), (57.5, 10), (63.5, 0). Connect these points with straight line segments.
5. Add a legend to the graph to clearly show which polygon represents Team A and which represents Team B.
The resulting graph will show two frequency polygons comparing the runs scored by Team A and Team B over the first 60 balls.
Question 8. A random survey of the number of children of various age groups playing in a park was found as follows:
| Age (in years) | Number of children |
|---|---|
| 1 - 2 | 5 |
| 2 - 3 | 3 |
| 3 - 5 | 6 |
| 5 - 7 | 12 |
| 7 - 10 | 9 |
| 10 - 15 | 10 |
| 15 - 17 | 4 |
Draw a histogram to represent the data above.
Answer:
Given:
A frequency distribution table showing the age groups of children in a park and the number of children in each group.
| Age (in years) | Number of children |
| 1 - 2 | 5 |
| 2 - 3 | 3 |
| 3 - 5 | 6 |
| 5 - 7 | 12 |
| 7 - 10 | 9 |
| 10 - 15 | 10 |
| 15 - 17 | 4 |
To Draw:
A histogram to represent the given data.
Solution:
To draw a histogram, the class intervals must be continuous. The given intervals (1-2, 2-3, 3-5, etc.) are continuous because the upper limit of one class is the lower limit of the next. However, the class widths are unequal:
- Class 1 - 2: Width = $2 - 1 = 1$ year
- Class 2 - 3: Width = $3 - 2 = 1$ year
- Class 3 - 5: Width = $5 - 3 = 2$ years
- Class 5 - 7: Width = $7 - 5 = 2$ years
- Class 7 - 10: Width = $10 - 7 = 3$ years
- Class 10 - 15: Width = $15 - 10 = 5$ years
- Class 15 - 17: Width = $17 - 15 = 2$ years
When class widths are unequal, the areas of the rectangles in the histogram should be proportional to the frequencies. This means we need to adjust the height of the rectangles. The height is calculated as:
Height of the rectangle (Adjusted Frequency) $= \frac{\text{Frequency}}{\text{Width of the class}} \times \text{Minimum class width}$
The minimum class width is 1 year.
Let's calculate the adjusted frequency for each class:
- For class 1 - 2: Adjusted Frequency $= \frac{5}{1} \times 1 = 5$
- For class 2 - 3: Adjusted Frequency $= \frac{3}{1} \times 1 = 3$
- For class 3 - 5: Adjusted Frequency $= \frac{6}{2} \times 1 = 3$
- For class 5 - 7: Adjusted Frequency $= \frac{12}{2} \times 1 = 6$
- For class 7 - 10: Adjusted Frequency $= \frac{9}{3} \times 1 = 3$
- For class 10 - 15: Adjusted Frequency $= \frac{10}{5} \times 1 = 2$
- For class 15 - 17: Adjusted Frequency $= \frac{4}{2} \times 1 = 2$
To draw the histogram:
1. Draw the horizontal axis (x-axis) and label it 'Age (in years)'. Mark the class boundaries (1, 2, 3, 5, 7, 10, 15, 17) along the axis. Since the first class starts at 1, you can start the axis from 0 or 1, ensuring the first rectangle's base is from 1 to 2.
2. Draw the vertical axis (y-axis) and label it 'Adjusted Frequency' or 'Frequency per unit width'. Choose a suitable scale for the adjusted frequencies. The adjusted frequencies are 5, 3, 3, 6, 3, 2, 2. A scale from 0 to 7 with increments of 1 would be appropriate.
3. Draw rectangles for each class interval. The base of each rectangle will be the width of the class interval on the x-axis, and the height will be the calculated adjusted frequency for that class.
- Draw a rectangle with base from 1 to 2 on the x-axis and height 5 on the y-axis.
- Draw a rectangle with base from 2 to 3 on the x-axis and height 3 on the y-axis.
- Draw a rectangle with base from 3 to 5 on the x-axis and height 3 on the y-axis.
- Draw a rectangle with base from 5 to 7 on the x-axis and height 6 on the y-axis.
- Draw a rectangle with base from 7 to 10 on the x-axis and height 3 on the y-axis.
- Draw a rectangle with base from 10 to 15 on the x-axis and height 2 on the y-axis.
- Draw a rectangle with base from 15 to 17 on the x-axis and height 2 on the y-axis.
The rectangles must be adjacent, with their bases covering the exact range of the continuous class intervals on the x-axis.
Question 9. 100 surnames were randomly picked up from a local telephone directory and a frequency distribution of the number of letters in the English alphabet in the surnames was found as follows:
| Number of letters | Number of surnames |
|---|---|
| 1 - 4 | 6 |
| 4 - 6 | 30 |
| 6 - 8 | 44 |
| 8 - 12 | 16 |
| 12 - 20 | 4 |
(i) Draw a histogram to depict the given information.
(ii) Write the class interval in which the maximum number of surnames lie.
Answer:
Given:
A frequency distribution table showing the number of letters in 100 surnames and the count of surnames for each range of letters.
| Number of letters | Number of surnames |
| 1 - 4 | 6 |
| 4 - 6 | 30 |
| 6 - 8 | 44 |
| 8 - 12 | 16 |
| 12 - 20 | 4 |
To Do:
(i) Draw a histogram to depict the given information.
(ii) Write the class interval in which the maximum number of surnames lie.
Solution:
Part (i): Draw a histogram
To draw a histogram, we first need to ensure the class intervals are continuous. The given intervals (1-4, 4-6, etc.) appear to be continuous in nature, where 4 is the upper boundary of the first class and the lower boundary of the second. However, the class widths are unequal:
- Class 1 - 4: Width = $4 - 1 = 3$ letters
- Class 4 - 6: Width = $6 - 4 = 2$ letters
- Class 6 - 8: Width = $8 - 6 = 2$ letters
- Class 8 - 12: Width = $12 - 8 = 4$ letters
- Class 12 - 20: Width = $20 - 12 = 8$ letters
The minimum class width is 2 letters.
When class widths are unequal, the heights of the rectangles in the histogram must be adjusted so that the area of each rectangle is proportional to the frequency. The adjusted height is calculated as:
Height of the rectangle (Adjusted Frequency) $= \frac{\text{Frequency of the class}}{\text{Width of the class}} \times \text{Minimum class width}$
Here, the minimum class width is 2.
Let's calculate the adjusted frequency for each class:
- For class 1 - 4: Adjusted Frequency $= \frac{6}{3} \times 2 = 2 \times 2 = 4$
- For class 4 - 6: Adjusted Frequency $= \frac{30}{2} \times 2 = 30 \times 1 = 30$
- For class 6 - 8: Adjusted Frequency $= \frac{44}{2} \times 2 = 44 \times 1 = 44$
- For class 8 - 12: Adjusted Frequency $= \frac{16}{4} \times 2 = 4 \times 2 = 8$
- For class 12 - 20: Adjusted Frequency $= \frac{4}{8} \times 2 = \frac{1}{2} \times 2 = 1$
To draw the histogram:
1. Draw the horizontal axis (x-axis) and label it 'Number of letters'. Mark the class boundaries (1, 4, 6, 8, 12, 20) on this axis. The segments between these marks should be proportional to the class widths (e.g., the distance from 1 to 4 is wider than from 4 to 6 or 6 to 8).
2. Draw the vertical axis (y-axis) and label it 'Adjusted Frequency' or 'Frequency per unit width'. Choose a suitable scale for the adjusted frequencies. The adjusted frequencies are 4, 30, 44, 8, 1. A scale from 0 to 50 with increments of 5 or 10 would be appropriate.
3. Draw rectangles over each class interval. The base of each rectangle is the corresponding class interval on the x-axis, and the height is the calculated adjusted frequency.
- Draw a rectangle with base from 1 to 4 on the x-axis and height 4 on the y-axis.
- Draw a rectangle with base from 4 to 6 on the x-axis and height 30 on the y-axis.
- Draw a rectangle with base from 6 to 8 on the x-axis and height 44 on the y-axis.
- Draw a rectangle with base from 8 to 12 on the x-axis and height 8 on the y-axis.
- Draw a rectangle with base from 12 to 20 on the x-axis and height 1 on the y-axis.
The rectangles must be adjacent.
Part (ii): Class interval with maximum number of surnames
To find the class interval that contains the maximum number of surnames, we simply look at the 'Number of surnames' column in the original table and find the highest frequency.
The frequencies are:
- 1 - 4: 6 surnames
- 4 - 6: 30 surnames
- 6 - 8: 44 surnames
- 8 - 12: 16 surnames
- 12 - 20: 4 surnames
The highest frequency is 44.
This frequency corresponds to the class interval 6 - 8.
Therefore, the class interval in which the maximum number of surnames lie is 6 - 8.

